Palindrome Sub String
Given a string s, return the longest palindromic substring in s.
Example 1:
Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer
Example 2:
Input: s = "cbbd"
Output: "bb"
Constrains:
1)1<=s.length <= 1000
2)s consists of only digits and english letters
Sample input
babad
Sample output:
bab
Program:
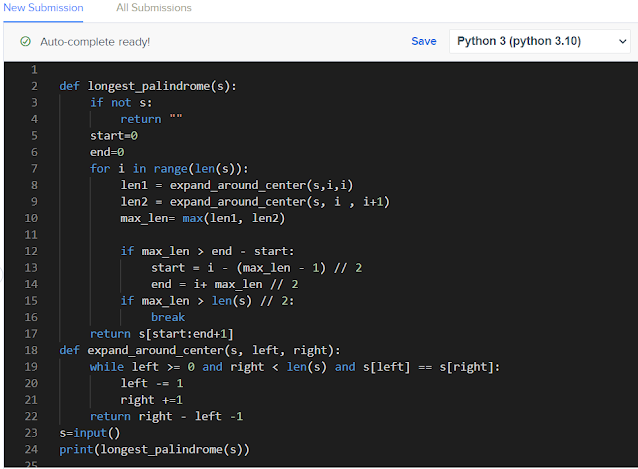
def longest_palindrome(s):
if not s:
return ""
start = 0
end = 0
for i in range(len(s)):
len1 = expand_around_center(s, i, i)
len2 = expand_around_center(s, i, i + 1)
max_len = max(len1, len2)
if max_len > end - start:
start = i - (max_len - 1) // 2
end = i + max_len // 2
# Prioritize inner palindromes by breaking when we find a palindrome of more than half the string's length
if max_len > len(s) // 2:
break
return s[start:end+1]
def expand_around_center(s, left, right):
while left >= 0 and right < len(s) and s[left] == s[right]:
left -= 1
right += 1
return right - left - 1
# Taking input from the user
s = input()
print(longest_palindrome(s))
Explanation:
Objective:
The goal is to find the longest palindromic substring within a given input string.
Base Condition:
If the input string is empty, return an empty string.
Initialization:
Initialize two pointers, start and end, to mark the beginning and end of the longest palindromic substring found.
Loop:
1)Iterate through each character in the input string using a loop.
2)For each character:
1)Treat it as a center and expand outwards:
1)Calculate the length of the palindrome when considering this character as the center.
2)Calculate the length of the palindrome when considering this character and its next character as the center.
2)Determine the maximum length of the palindromic substring found by comparing the lengths calculated in the previous step.
Updating Pointers:
1)If the maximum length found is greater than the difference between the current start and end, update the start and end pointers to mark the new longest palindromic substring's beginning and end.
Optimization:
1)If, at any point, the maximum length of a palindrome found is greater than half the length of the input string, break out of the loop.
2)This optimization is based on the observation that you won't find a longer palindrome with a future center if its length is already greater than half of the string's length.
Return Result:
1)Return the substring of the input string from index start to index end + 1 as the longest palindromic substring.
Helper Function: expand_around_center:
1)This function takes a string and two indices, left and right, as input.
2)It expands around the center defined by left and right as long as the characters at these positions are the same, effectively marking a palindrome.
3)The function returns the length of the palindrome found.
Conclusion:
1)The approach utilizes the concept of palindrome expansion around centers to efficiently identify and extract the longest palindromic substring within the given string.




0 Comments